- Accueil
- Unité 1
-
-
Partez à la découverte de la pratique fondée sur les données probantes
- Une formation : un bon départ!
- Le changement de paradigme dans la pratique
- Les facteurs qui ont mené à l’émergence de la pratique fondée sur les données probantes (PFDP)
- De quoi parle-t-on?
- Des arguments pour la PFDP
- Les défis... comment les contourner?
- Question de réflexion
- Concepts clés
-
-
- Unité 2
-
-
Intégrer la pratique fondée sur les données probantes en cinq étapes
- Étape 1 : Formuler une bonne question clinique
- Étape 2 : Chercher les preuves scientifiques
- Étape 3 : Critiquer des articles scientifiques
- Étape 4 : Appliquer les résultats à la pratique
- Étape 5 : Évaluer le processus de décision clinique
-
-
- Unité 3
-
- Êtes-vous à l’aise avec les stats?
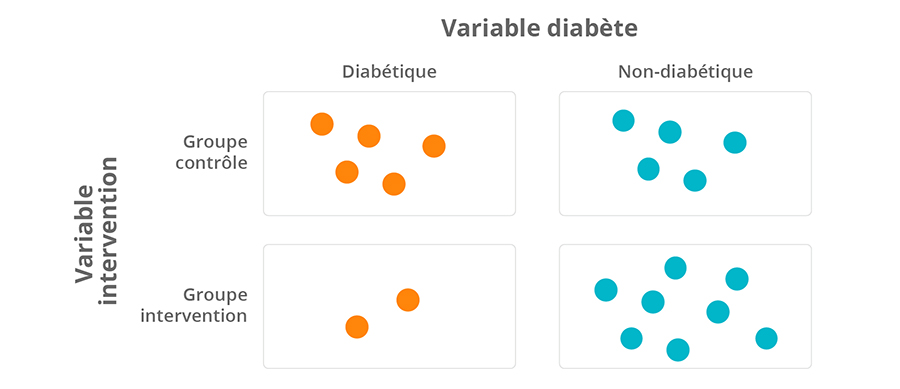
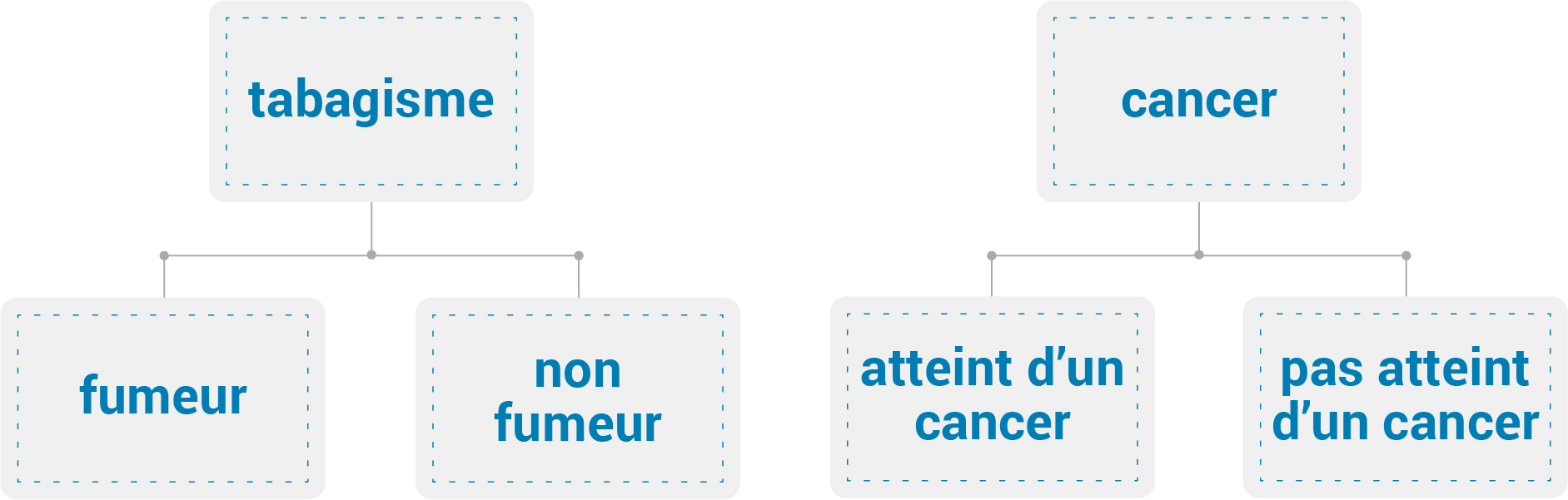
- Qu’est-ce qu’une variable?
- Ce que disent les variables
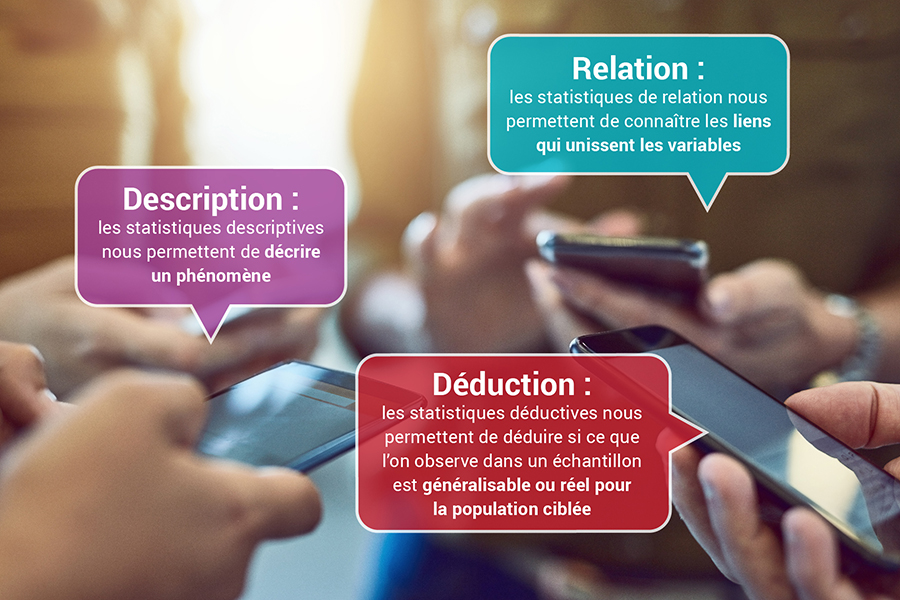
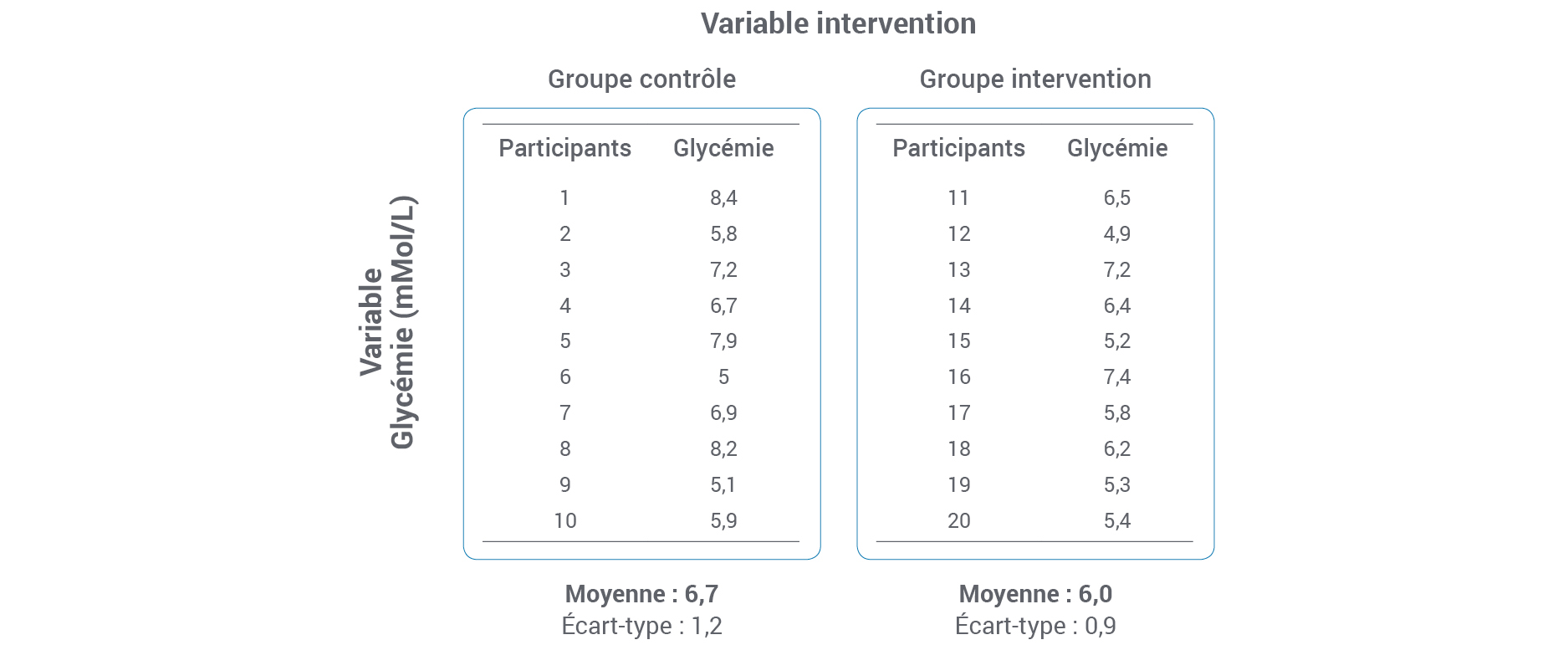
- En quoi consistent les statistiques descriptives?
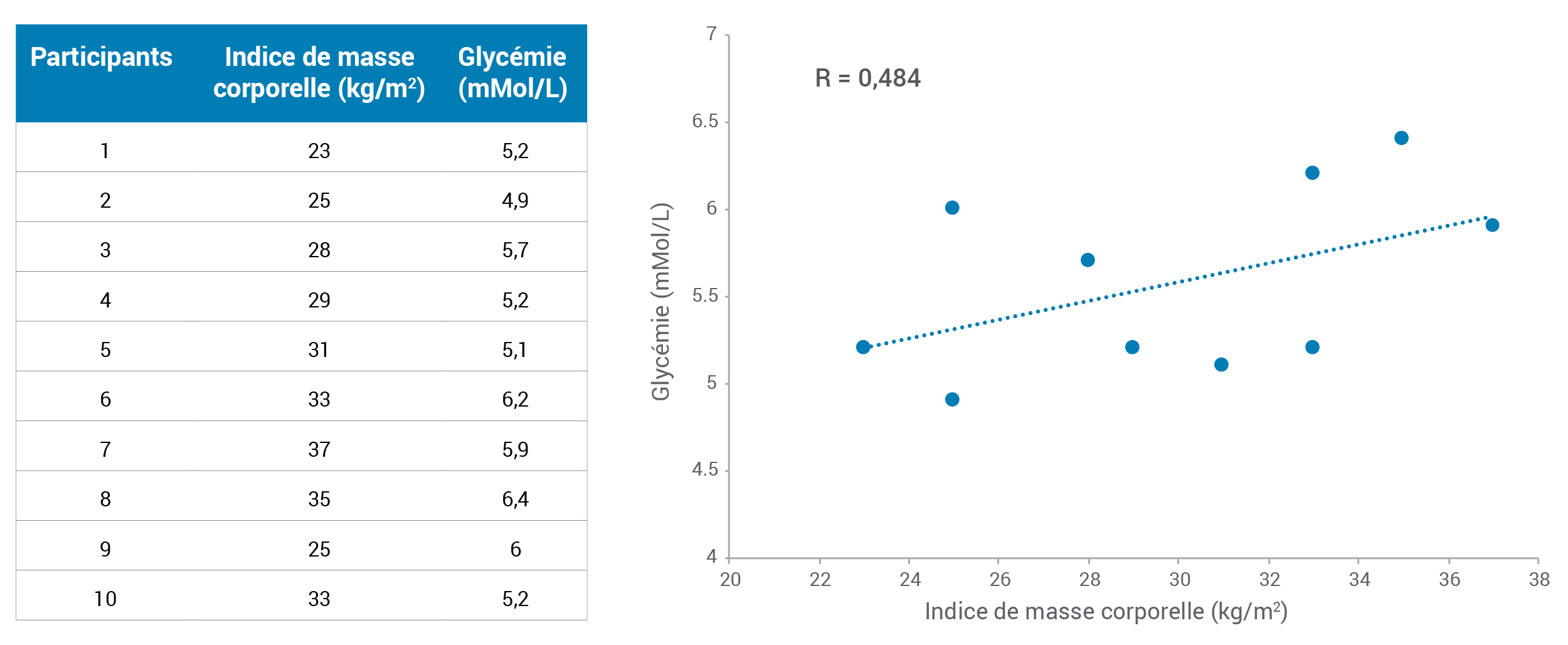
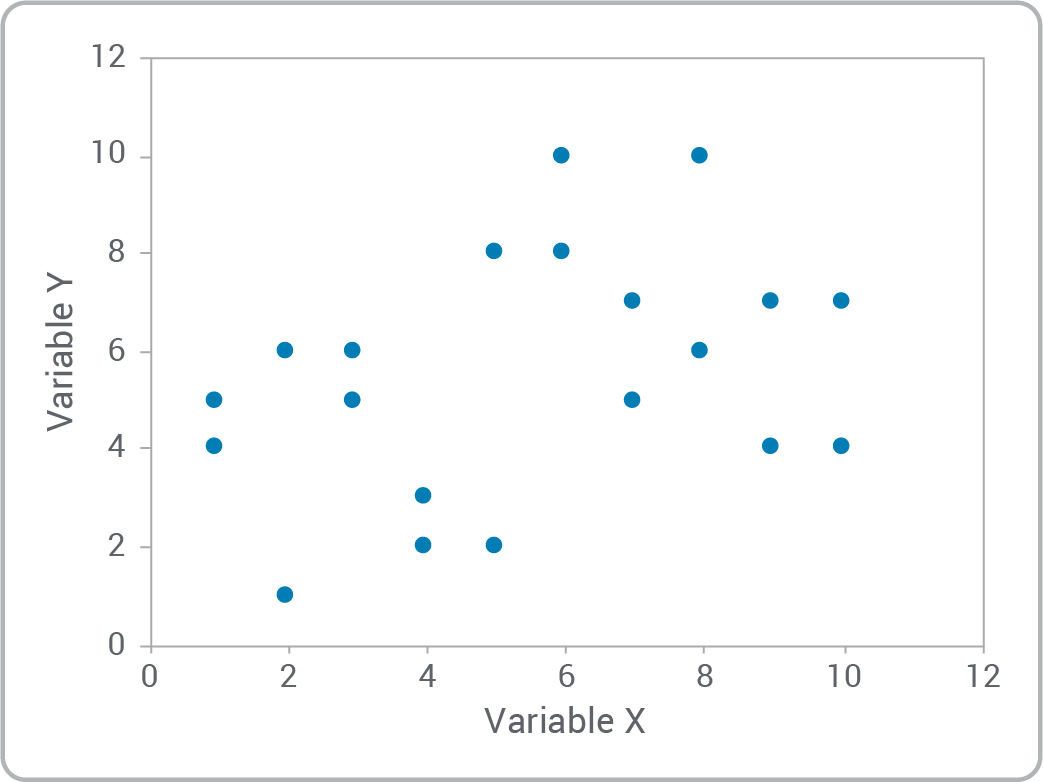
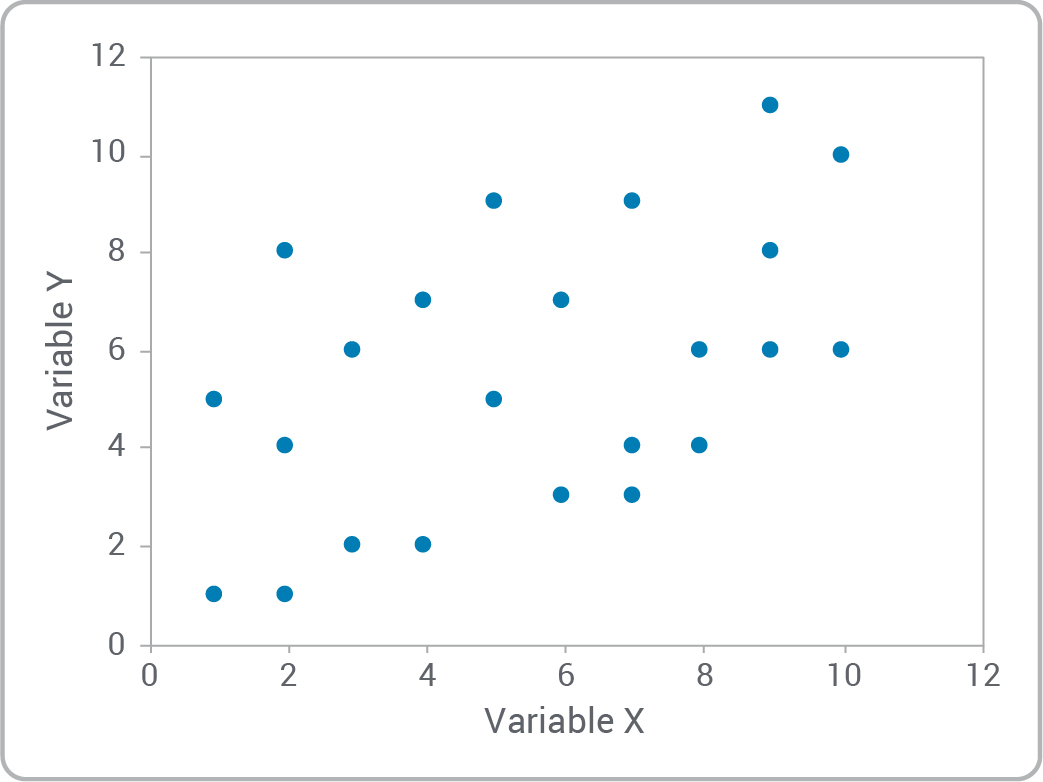
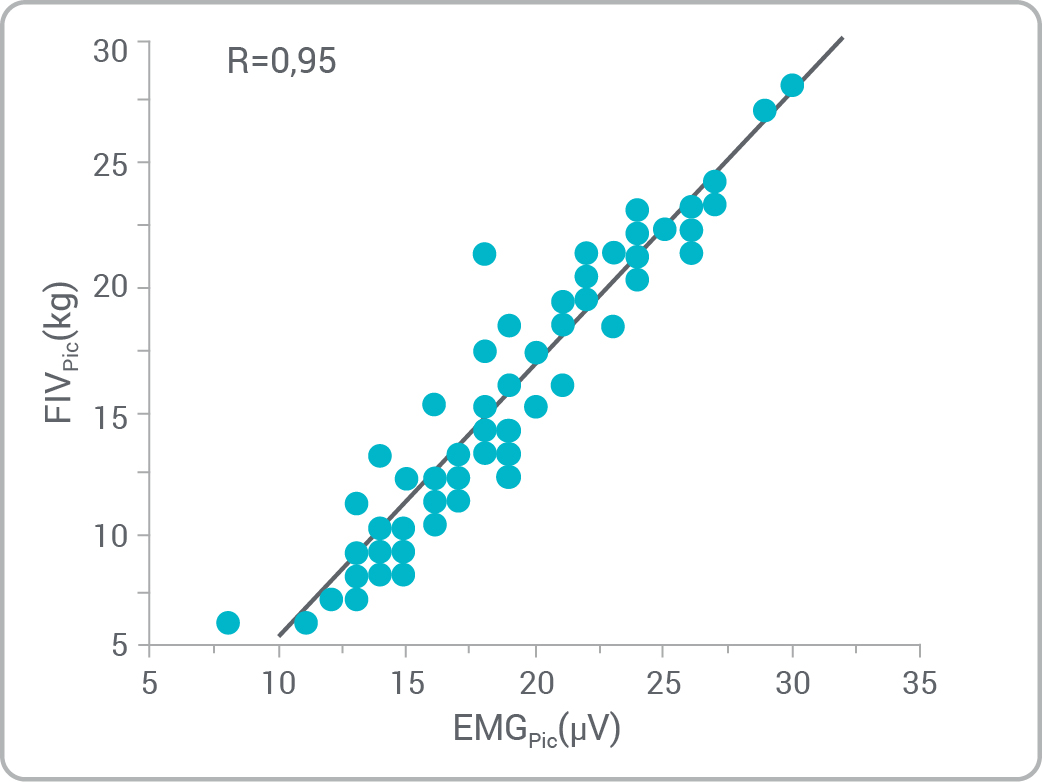
- Est-ce qu’il existe une relation entre les variables?
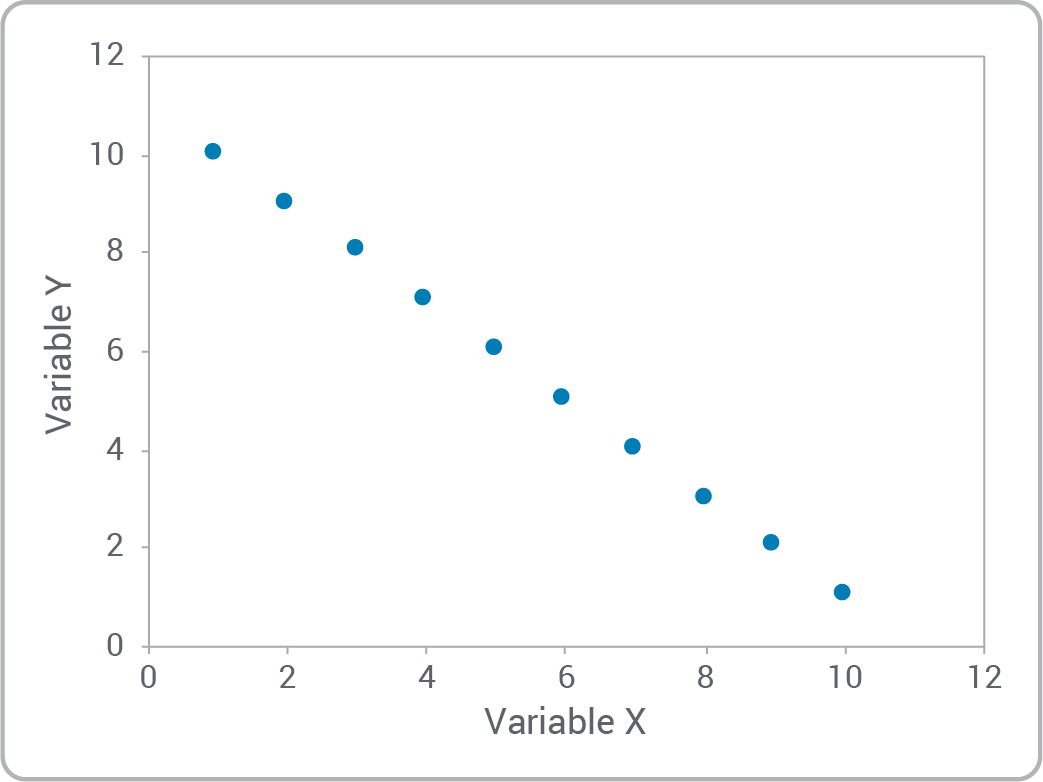
- Pouvez-vous reconnaître les types de relations?
- Prêt à relever le défi?
- Statistiquement significatif ou cliniquement significatif?
- Concepts clés
- Conclusion
Obtenir votre attestation
- Évaluation de l'atelier
- Examen final
-
- Ressources
-